Một người điều khiển thuyền đi được 5,6 km theo hướng Bắc trong 1,0 h. Sau đó quay thuyền về phía tây 3,4 km trong 30,0 phút. Tìm độ dịch chuyển tổng hợp và vận tốc trung bình.
Dạng bài: Vật lý 10. Một người điều khiển thuyền đi được 5,6 km theo hướng Bắc trên mặt hồ phẳng lặng trong thời gian 1,0 h. Sau đó, anh ta quay thuyền đi về phía Tây 3,4 km trong 30,0 phút. Hướng dẫn chi tiết.
Một người điều khiển thuyền đi được 5,6 km theo hướng Bắc trên mặt hồ phẳng lặng trong thời gian 1,0 h. Sau đó, anh ta quay thuyền đi về phía Tây 3,4 km trong 30,0 phút.
a) Tìm độ dịch chuyển tổng hợp của thuyền.
b) Xác định vận tốc trung bình của chuyến đi.
Công thức liên quan
Vận tốc trung bình
Vật lý 10. Vận tốc trung bình trong chuyển động thẳng. Hướng dẫn chi tiết.
a/Định nghĩa:
Vận tốc trung bình là thương số giữa độ dời (độ dịch chuyển) vật di chuyển được và thời gian di chuyển hết độ đời đó.
b/Công thức
Chú thích:
: vận tốc trung bình của vật (m/s).
: độ dời của vật (m).
: độ dịch chuyển của vật (m)
: thời gian chuyển động của vật (s).
: tọa độ của vật ở vị trí 1 và 2 (m)
: thời điểm 1 và 2 trong chuyển động của vật (s)
Lưu ý
+ Vận tốc trung bình có thể âm hoặc dương tùy theo cách chọn chiều dương. Khi chọn chiều dương cùng chiều chuyển động vận tốc trung bình mang giá trị dương. Ngược lại, khi chọn chiều dương ngược chiều chuyển động vận tốc trung bình mang giá trị âm.
+ Vận tốc trung bình qua hai tọa độ có độ lớn giống nhau trong mọi hệ quy chiếu.
+ Một vật đi A đến B rồi từ B về A thì vận tốc trung bình trên cả quá trình bằng không dù đi trên đoạn đường với vận tốc khác nhau. Lúc này vận tốc trung bình không thể hiện được mức độ nhanh chậm của chuyển động.
Độ dịch chuyển
Vật lý 10. Độ dịch chuyển. Hướng dẫn chi tiết.
- Độ dịch chuyển là một vectơ, cho biết độ dài và hướng của sự thay đổi vị trí của vật.
- Độ dịch chuyển được biểu diễn bằng một mũi tên nối vị trí đầu và vị trí cuối của chuyển động, có độ dài tỉ lệ với độ lớn của độ dịch chuyển.
- Kí hiệu:
- Đơn vị: mét (m)
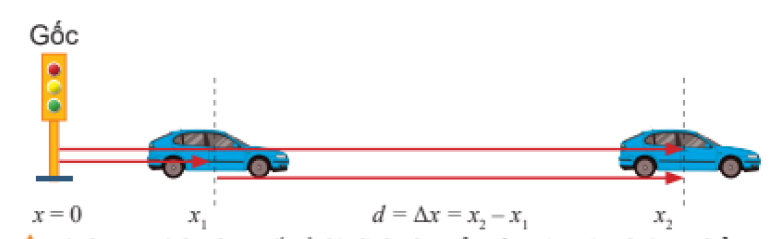
- Độ dịch chuyển là một đại lượng có thể nhận giá trị âm, dương hoặc bằng không. Trong khi quãng đường đi được là một đại lượng không âm.
Biến số liên quan
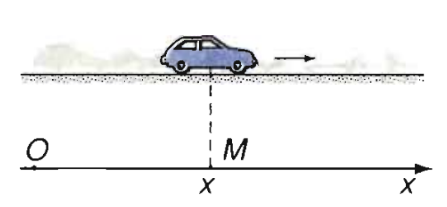
Tọa độ trong chuyển động thẳng - Vật lý 10
Vật lý 10. Tọa độ là gì? Cách xác định tọa độ của một vật trong chuyển động. Hướng dẫn chi tiết.
Khái niệm:
Tọa độ là một tập hợp được sắp các con số nhằm xác định vị trí của một vật trong không gian, một phần tử trong hệ thống. Toạ độ được sử dụng trong vật lý và toán học.
Trong vật lý tọa độ thường được kí hiệu là .
Ngoài ra, để dễ quản lý, người ta còn đánh dấu tọa độ theo từ trạng thái.
Ví dụ:
: tọa độ đầu tiên của vật.
: tọa độ tại vị trí thứ 1.
: tọa độ tại vị trí thứ 2.
Đơn vị tính: mét (m)
Độ dời trong chuyển động thẳng (độ dịch chuyển) - Vật lý 10
Vật lý 10.Độ dời là gì? Hướng dẫn chi tiết.
Khái niệm:
Độ dời trong chuyển động thẳng là hiệu số giữa hai tọa độ.
Độ dời có thể âm, có thể dương, cũng có thể bằng không tùy thuộc vào từng trường hợp.
Đơn vị tính: mét (m)

Vận tốc trung bình - Vật lý 10
Vật lý 10.Vận tốc trung bình là gì? Hướng dẫn chi tiết.
Khái niệm:
Vận tốc trung bình được hiểu là thương số giữa độ dời mà vật đi được và khoảng thời gian vật thực hiện độ dời đó.
Đơn vị tính: hoặc .
Thời gian - Vật lý 10
Vật lý 10. Thời gian của chuyển động. Hướng dẫ chi tiết.
Khái niệm:
Thời gian t là thời gian vật tham gia chuyển động từ vị trí này đến vị trí khác theo phương chuyển động của vật.
Đơn vị tính: giây (s), phút (min), giờ (h).
Độ biến thiên thời gian - Vật lý 10
Vật lý 10. Độ biến thiên thời gian. Hướng dẫn chi tiết.
Khái niệm:
Độ biến thiên thời gian là hiệu số giữa hai thời điểm và .
Đơn vị tính: giây (s), phút (min), giờ (h).
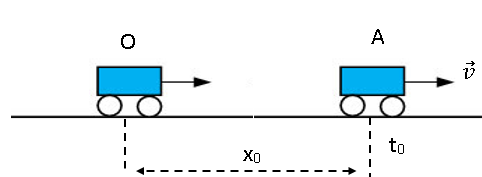
Tọa độ ban đầu trong chuyển động thẳng - Vật lý 10
Vật lý 10. Tọa độ ban đầu là gì? Cách xác định tọa độ của một vật trong chuyển động. Hướng dẫn chi tiết.
Khái niệm:
là tọa độ ban đầu của vật tại thời điểm ban đầu (t = 0).
Đơn vị tính: mét ()
Các câu hỏi liên quan
Một vật m trượt không ma sát, không vận tốc đầu từ đỉnh một dốc nghiêng dài 17,3 m và nghiêng góc 60 so với phương ngang. Tính tốc độ của vật khi trượt hết dốc.
- Tự luận
- Độ khó: 0
Một vật m trượt không ma sát, không vận tốc đầu từ đỉnh một dốc nghiêng dài 17,3 m và nghiêng góc so với phương ngang. Tính tốc độ của vật khi trượt hết dốc. Lấy g =10 m/.
Một quả cầu m được cung cấp với vận tốc bằng 8 m/s tại chân dốc để đi lên một dốc nghiêng dài, có góc nghiêng 30 độ. Hãy xác định vị trí cao nhất mà vật có thể đạt được.
- Tự luận
- Độ khó: 0
Một quả cầu m được cung cấp với vận tốc bằng 8 m/s tại chân dốc để đi lên một dốc nghiêng dài, có góc nghiêng so với mặt phẳng ngang. Bỏ qua ma sát, lấy g = 10 m/.
a/ Hãy xác định vị trí cao nhất mà vật có thể đạt được.
b/ Tính quãng đường dài nhất mà vật đi được trên dốc.
Một vật có khối lượng m trượt không vận tốc đầu từ đỉnh một mặt phẳng nghiêng dài 10 m. Hãy tính vận tốc của vật ở chân mặt phẳng nghiêng trong hai trường hợp.
- Tự luận
- Độ khó: 0
Một vật có khối lượng m trượt không vận tốc đầu từ đỉnh một mặt phẳng nghiêng dài 10 m, nghiêng một góc 30° so với mặt phẳng nằm ngang. Lấy g = 10 m/. Hãy tính vận tốc của vật ở chân mặt phẳng nghiêng trong hai trường hợp:
a/ Vật trượt không ma sát.
b/ Vật trượt có ma sát với hệ số ma sát là 0,1.
Quả cầu nhỏ m treo ở đầu một sợi dây dài 50 cm, đầu trên của dây cố định. Tính độ cao cực đại mà vật m đạt được. Tính góc lệch lớn nhất của dây treo hợp với phương thẳng đứng.
- Tự luận
- Độ khó: 0
Quả cầu nhỏ m treo ở đầu một sợi dây dài 50 cm, đầu trên của dây cố định. Vật m đang đứng yên thì được cung cấp vận tốc v = 2 m/s theo phương ngang. Lấy g = 10 m/.
a/ Tính độ cao cực đại mà vật m đạt được.
b/ Tính góc lệch lớn nhất của dây treo hợp với phương thẳng đứng.
Một vật khối lượng 1 kg được thả rơi tự do từ độ cao 20 m tại nơi có g = 10 m/s2. Dùng kiến thức về sự rơi tự do, hãy tính vận tốc của vật lúc chạm đất.
- Tự luận
- Độ khó: 0
Một vật khối lượng 1 kg được thả rơi tự do từ độ cao 20 m tại nơi có g = 10 m/.
a) Dùng kiến thức về sự rơi tự do, hãy tính vận tốc của vật lúc chạm đất.
b) Tính cơ năng của vật lúc bắt đầu thả và cơ năng của vật lúc chạm đất. So sánh cơ năng ở hai vị trí này.
c) Tính vận tốc vật tại độ cao 10 m bằng phương pháp sử dụng định luật bảo toàn cơ năng.