Một lăng kính tam giác cân ABC có góc đinh chiết suất đối với ánh sáng đỏ và tím lần lượt là , . Chiếu tới mặt bên AB một tia sáng trắng vuông góc với AB , điểm tới rất gần B . Sau khi qua lăng kính ánh sáng ló là :
Hằng số liên quan
Chiết suất của một số môi trường
Vật lý 11.Chiết suất của một số môi trường. Hướng dẫn chi tiết.
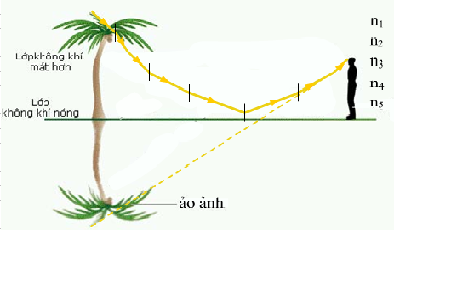
Chiết suất cũng thay đổi ở những lớp không khí có có sự chênh lệch nhiệt độ.
Biến số liên quan
Góc tới
Vật lý 11.Góc tới. Hướng dẫn chi tiết.
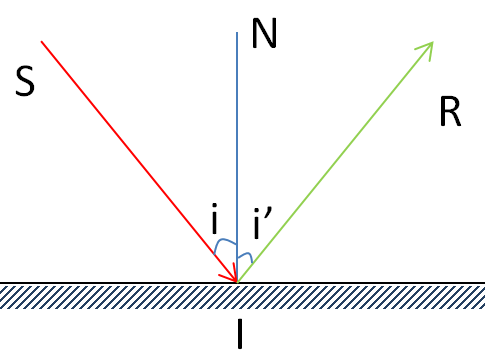
Khái niệm:
Góc tới là góc tạo bởi tia tới và pháp tuyến của mặt phẳng phân cách giữa hai môi trường.
Đơn vị tính: Degree () hoặc Radian
Góc giới hạn toàn phần
Góc giới hạn phản xạ toàn phần. Vật Lý 11.
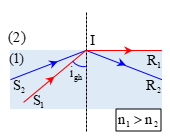
Khái niệm:
Khi góc i tăng thì góc r cũng tăng (với r > i) nên khi r đạt giá trị cực đại thì i đạt giá trị gọi là góc giới hạn phản xạ toàn phần, còn gọi là góc tới hạn.
Đơn vị tính: Degree () hoặc Radian
Chiết suất của môi trường với ánh sáng đỏ - Vật lý 12
Vật lý 12. Chiết suất của môi trường với ánh sáng đỏ. Hướng dẫn chi tiết.
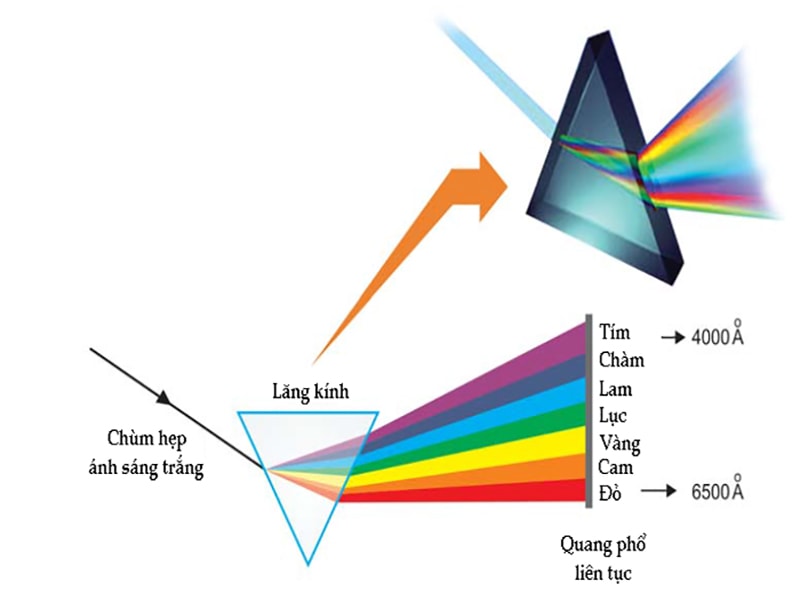
Khái niệm:
- Chiết suất của môi trường với ánh sáng đỏ được xác định bằng vận tốc của ánh sáng đỏ trong môi trường đó chia cho vận tốc ánh sáng trong chân không.
- Chiết suất của môi trường giải thích được hiện tượng tán sắc ánh sáng qua lăng kính do sự khác nhau về chiết suất của của các màu với lăng kính.
Đơn vị tính: không có
Các câu hỏi liên quan
Một quả cầu bằng sắt có thể tích 4 dm^3 được nhúng chìm trong nước, biết khối lượng riêng của nước 1000 kg/m^3.
- Tự luận
- Độ khó: 2
- Video
Một quả cầu bằng sắt có thể tích 4 dm3 được nhúng chìm trong nước, biết khối lượng riêng của nước 
. Lực đẩy Archimedes tác dụng lên quả cầu là
A. 4000 N.
B. 40000 N.
C. 2500 N.
D. 40 N.
Một vật nặng 3600 g có khối lượng riêng bằng 1800 kg/m^3. Khi thả vào chất lỏng có khối lượng riêng bằng 850 kg/m^3, vật hoàn toàn nằm dưới mặt chất lỏng.
- Tự luận
- Độ khó: 1
- Video
Một vật nặng 3600 g có khối lượng riêng bằng 
. Khi thả vào chất lỏng có khối lượng riêng bằng 
, vật hoàn toàn nằm dưới mặt chất lỏng. Vật đã chiếm chỗ chất lỏng có thể tích bằng
A. 
.
B. 
.
C. 
.
D. 
.
Một quả năng làm bằng sắt nặng 50 g, có thể tích 25 cm^3 được nhúng chìm trong nước.
- Tự luận
- Độ khó: 1
- Video
Một quả nặng làm bằng sắt nặng 50 g, có thể tích 
được nhúng chìm trong nước. Khối lượng riêng của nước là 
. Lực đẩy Archimedes tác dụng lên vật là
A. 0,5 N.
B. 0,25 N.
C. 0,05 N.
D. 2,5 N.
Một vật có thể tích 0,1 m^3 và trọng lượng 2500 N.
- Tự luận
- Độ khó: 2
- Video
Một vật có thể tích 
và trọng lượng 2500 N. Để giữ vật cân bằng trong nước phải tác dụng lên vật một lực có phương thẳng đứng hướng từ dưới lên trên và có độ lớn là bao nhiêu? Biết 
.
A. 2500 N.
B. 1000 N.
C. 1500 N.
D. > 2500 N.
Một quả cầu bằng sắt có thể tích 2 dm^3 được nhúng chìm trong nước, biết khối lượng riêng của nước 1000 kg/m^3.
- Tự luận
- Độ khó: 1
- Video
Một quả cầu bằng sắt có thể tích 
được nhúng chìm trong nước, biết khối lượng riêng của nước 
. Lực đẩy Archimedes tác dụng lên quả cầu là
A. 2000 N.
B. 20000 N.
C. 200 N.
D. 20 N.